まずベイズの定理とベイズ推定について説明します。
ベイズの定理とは、Aという事象が起こった場合に、Bの事象が起こる確率など、ある条件下での確率である、条件確率について適用できる定理で、以下の式のような単純な形で表されます。
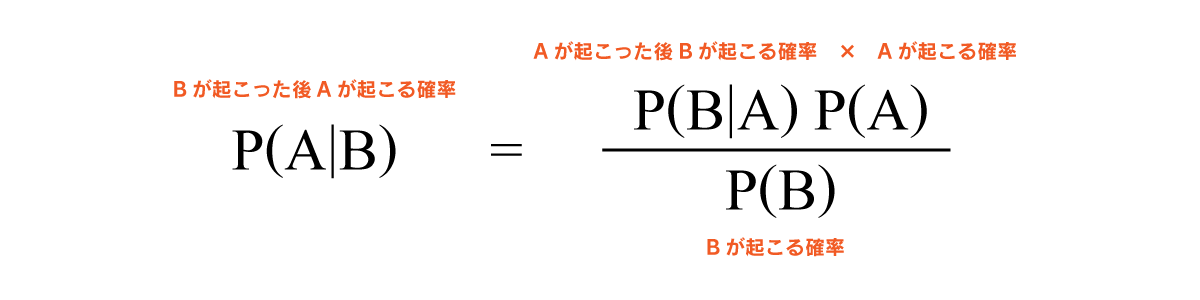
この式は「Bが起こった後にAが起こる条件確率」は、「Aが起こった後にBが起こる条件確率」に、「Aが起こる確率」を掛け合わせたものを、「Bが起こる確率」で割ったものになります。何かの原因で結果が生じた場合、原因を解析して結果を推定するのが通常の流れですが、ベイズの定理では、結果を解析して原因を突き止めるという時間逆行の推定を可能にしていることが大きな特徴と言えます。そして、このベイズの定理を使用して、観測された事象から、推定したい事柄を確率的に推定する事をベイズ推定と呼びます。※ベイズでは確率を一つの値としてではなく、分布として持っています。
ベイズ推定の中でも、階層ベイズモデルは「標本が一意の確率である、というスタンスではなく、個体ごとに確率が違う」と捉え、個体ごとの確率は「全体に共通する部分と個体差があり、その分布に従って決まる」という前提で推定を行います。
例えばコインの表が出る確率(表率)で考えた場合、標本となるコインが大量にあったとすると、それぞれのコインは大きさや歪みなどがあり、それらが影響して少しずつ表率には差が生じ、一定ではないことが考えられます。そのとき、表率はだいたい1/2だろうという共通の部分と、大きさ等が影響した個体差の部分に分けられます。これらの確率分布が分かれば、個々の表率を決める確率分布が決まり、コインそれぞれの表率が決まるという流れで推定することが出来ます。(ここでは詳細な説明は割愛しますが、MCMCという手法を用いて確率分布をサンプリングして推定していきます)
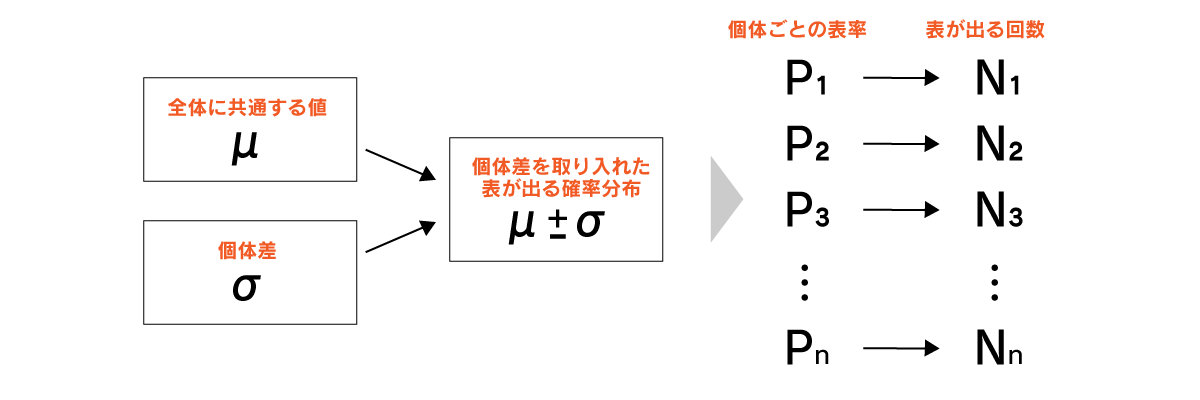
このコインの例を、顧客の購入回数や金額、ブランドの選択などに置き換え、会員の個人差が得られれば、ターゲティングに活用するなどのマイクロマーケティング応用が可能です。また、ブランド別の購買金額や顧客属性など、変数同士の関係を明らかにし構造を把握することにも可能です。
階層ベイズモデルにご興味のある方、詳しい説明が必要な方はこちらからお気軽にお問合せください。また、階層ベイズモデルを活用した事例をこちらでご紹介しています。







